O μεγαλύτερος πρώτος αριθμός

…. έχει 22,338,618 ψηφία

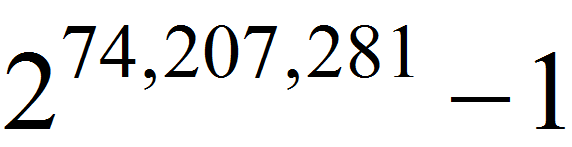Πρώτοι αριθμοί είναι οι αριθμοί που διαιρούνται μόνο με τον εαυτό τους και τη μονάδα, όπως οι 2, 3, 5, 7, 11, 13, κ.ο.κ.
Οι πρώτοι αριθμοί που γράφονται στη μορφή 2^ν-1, ονομάζονται πρώτοι του Mersenne, από το όνομα του Γάλλου μοναχού Marin Mersenne, τον πρώτο που διερεύνησε αριθμούς τέτοιες μορφής.
Το νέο ρεκόρ μεγαλύτερου πρώτου αριθμού επιτεύχθηκε πάλι από το πρόγραμμα GIMPS (Great Internet Mersenne Prime Search) το οποίο συνδέει χιλιάδες υπολογιστές στον κόσμο ψάχνοντας πρώτους αριθμούς.
Ένας υπολογιστής (του δικτύου GIMPS) στο Πανεπιστήμιο του Μισούρι στις ΗΠΑ κατέγραψε τον μεγαλύτερο μέχρι σήμερα πρώτο αριθμό, που γράφεται ως:
 2^74,207,281-1 και ονομάζεται M74207281. Πρόκειται για το 49ο πρώτο του Mersenne.
Ο αριθμός αυτός αποτελείται από 22,338,618 ψηφία και είναι κατά 5 εκατομμύρια ψηφία περίπου μακρύτερος από τον προηγούμενο μεγαλύτερο γνωστό πρώτο αριθμό 2^57,885,161-1.
To Gimps ξεκίνησε πριν από 20 χρόνια και (παρά το «ατυχές» όνομά του) κατάφερε να ανακαλύψει τους 15 μεγαλύτερους γνωστούς μέχρι σήμερα πρώτους αριθμούς.
Επόμενος στόχος των ερευνητών είναι το βραβείο των 150000 δολαρίων που προσφέρει το Electronic Frontier Foundation για την εύρεση πρώτου αριθμού με 100 εκατομμύρια ψηφία.
πηγή: http://www.mersenne.org

Υπενθυμίζεται ότι σύμφωνα με την απόδειξη του Ευκλείδη το σύνολο των πρώτων αριθμών είναι άπειρο:
«… Οι πρώτοι αποτελούν τους οικοδομικούς λίθους στο βασίλειο των αριθμών, γιατί όλοι οι άλλοι αριθμοί είναι σύνθετοι, εφόσον παράγονται παίρνοντας γινόμενα πρώτων. Ακόμα και η πιο επιπόλαια μελέτη αποκαλύπτει ότι οι πρώτοι αραιώνουν όπως προχωρούμε σε ολοένα μεγαλύτερους αριθμούς. Εγείρεται λοιπόν το ερώτημα: σταματούν κάπου; Δηλαδή υπάρχει κάποιος τελευταίος πρώτος και όλοι οι αριθμοί που τον ακολουθούν είναι σύνθετοι; Ο Ευκλείδης ήταν ο πρώτος που το απάντησε και μάλιστα κατά τον τέλειο τρόπο.
Κανένας ηλεκτρονικός υπολογιστής δεν θα μπορούσε να απαντήσει στο ερώτημα, εφόσον είναι ερώτημα που αφορά το άπειρο. Μόνο ο νους μπορούσε. Εδώ είναι λοιπόν η απόδειξη του Ευκλείδη. Ας υποθέσουμε ότι, τουναντίον, το σύνολο των πρώτων αριθμών είναι πεπερασμένο, επομένως μπορούμε να τους απαριθμήσουμε κατά αύξουσα τάξη, παραλείποντας την μονάδα:
p₁• p₂• … • p_n
Aς εξετάσουμε τότε τον αριθμό
Μ=Π+1
όπου Π είναι το γινόμενο
Π= p₁• p₂• … • p_n
Εφόσον ο Μ είναι μεγαλύτερος από τον τελευταίο πρώτο, τον p_n, πρέπει να είναι σύνθετος αριθμός. Επομένως, ο Μ έχει κάποιον πρώτο παράγοντα, ας πούμε τον q. Άρα ο q είναι ένας από τους p₁, p₂, … , p_n.
Ωστόσο, εάν q= p_k για κάποιο k=1, …, n, τότε, εφόσον ο q διαιρεί τον Μ και επίσης προφανώς διαιρεί το γινόμενο Π, κατ’ ανάγκη διαιρεί την διαφορά τους, δηλαδή την μονάδα. Τούτο όμως είναι άτοπο. Γιατί κανείς αριθμός, εκτός από την ίδια την μονάδα, δεν διαιρεί την μονάδα, και έχουμε παραλείψει την μονάδα από την παραπάνω απαρίθμηση.
Επομένως, το αντίθετο της αρχικής μας υποθέσεως πρέπει να ισχύει, δηλαδή το σύνολο των πρώτων αριθμών πρέπει να είναι άπειρο.
Όσο απλή κι αν φαίνεται αυτή η απόδειξη, θεωρείται ακόμα ως μια από τις κομψότερες σε όλα τα μαθηματικά. Ας σκεφτούμε τις επαναστάσεις στην ιστορία της σκέψεως που περιέχονται σε αυτό το απλό κομμάτι μαθηματικών.
Πρώτον, ότι ο νους μπορεί να θέσει ένα ερώτημα που αφορά το άπειρο . Δεύτερον, ότι ο νους μπορεί να δώσει την απάντηση κατά έναν καθοριστικό και μη αμφισβητήσιμο τρόπο. Τρίτον, ότι η αλήθεια βρίσκεται δείχνοντας ότι η αντίθετη υπόθεση οδηγεί σε άτοπο. Όλες οι μεγάλες αποδείξεις στα μαθηματικά από την εποχή του Ευκλείδη μέχρι σήμερα έχουν χρησιμοποιήσει την ευκλείδεια μέθοδο της εις άτοπον απαγωγής…»
–